Equação Do 2º Grau: O Que São, Tipos, Como Resolver? A equação do segundo grau é uma ferramenta matemática fundamental, presente em diversas áreas, desde a física e engenharia até a economia e finanças. Compreender seus conceitos, tipos e métodos de resolução é crucial para dominar problemas complexos e modelar situações reais. Neste texto, vamos explorar a fundo esse tema, desvendando seus mistérios e aplicando-o em exemplos práticos.
Começaremos definindo a forma geral da equação, diferenciando as equações completas e incompletas e explicando o significado de seus coeficientes (a, b, c). Em seguida, apresentaremos os principais métodos de resolução: a fórmula de Bhaskara, a fatoração e a soma e produto, comparando suas vantagens e desvantagens. A análise do discriminante (delta) e sua influência na natureza das raízes (reais e distintas, reais e iguais ou complexas) também será detalhada, juntamente com a relação entre o gráfico da função quadrática e as raízes da equação.
Conceitos Fundamentais da Equação do 2º Grau

A equação do 2º grau é um conceito fundamental da álgebra, com aplicações em diversas áreas, desde a física e engenharia até a economia e finanças. Compreender seus elementos e métodos de resolução é essencial para o domínio de conceitos matemáticos mais avançados.
A forma geral de uma equação do 2º grau é representada por:
ax² + bx + c = 0
, onde ‘a’, ‘b’ e ‘c’ são coeficientes numéricos, sendo ‘a’ diferente de zero (a ≠ 0). O coeficiente ‘a’ multiplica o termo quadrático (x²), ‘b’ multiplica o termo linear (x), e ‘c’ representa o termo constante.
Classificação das Equações do 2º Grau
As equações do 2º grau são classificadas como completas ou incompletas, dependendo dos valores dos coeficientes. Equações completas possuem todos os três coeficientes (a, b e c) diferentes de zero. Já as incompletas apresentam pelo menos um dos coeficientes ‘b’ ou ‘c’ igual a zero.
Raízes de uma Equação do 2º Grau
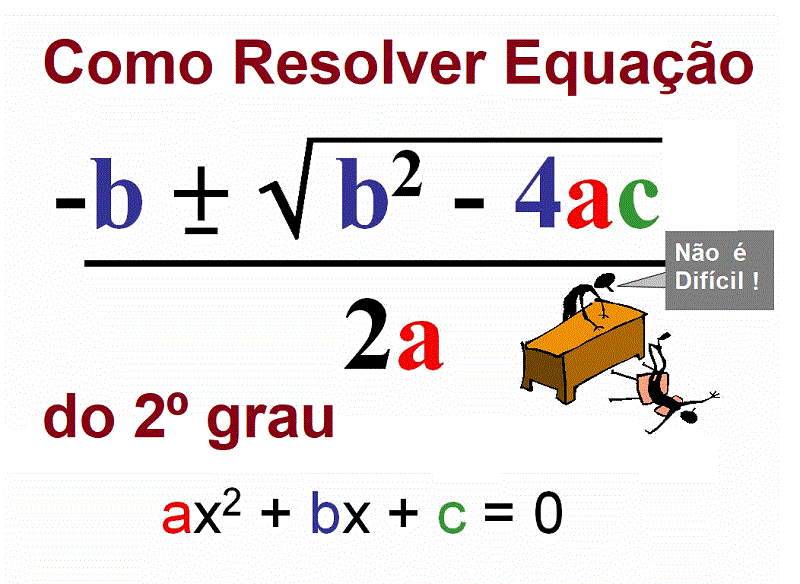
As raízes, ou soluções, de uma equação do 2º grau são os valores de ‘x’ que tornam a equação verdadeira. Uma equação do 2º grau pode ter duas raízes reais e distintas, duas raízes reais e iguais (uma raiz dupla) ou duas raízes complexas conjugadas. A existência e a natureza das raízes dependem do valor do discriminante (Δ), calculado pela fórmula:
Δ = b²-4ac
. Se Δ > 0, há duas raízes reais distintas; se Δ = 0, há uma raiz real dupla; e se Δ < 0, há duas raízes complexas conjugadas.
Exemplos de Equações do 2º Grau
A tabela abaixo apresenta exemplos de diferentes tipos de equações do 2º grau, ilustrando a variação dos coeficientes e a classificação de cada uma:
| a | b | c | Tipo de Equação |
|---|---|---|---|
| 2 | 5 | 3 | Completa |
| 1 | -4 | 0 | Incompleta (c = 0) |
| 3 | 0 | -9 | Incompleta (b = 0) |
| -1 | 2 | -1 | Completa |
Métodos de Resolução da Equação do 2º Grau: Equação Do 2º Grau: O Que São, Tipos, Como Resolver
A resolução de equações do segundo grau é fundamental em diversas áreas da matemática e suas aplicações. Existem diferentes métodos para encontrar as raízes (ou soluções) dessas equações, cada um com suas vantagens e desvantagens, dependendo das características da equação em questão. A escolha do método mais adequado depende da forma como a equação se apresenta, sendo algumas mais apropriadas para equações completas e outras para incompletas.
Comparação dos Métodos de Resolução
A fórmula de Bhaskara, a fatoração e a soma e produto são os métodos mais comuns para resolver equações do segundo grau. A fórmula de Bhaskara é um método geral, aplicável a qualquer equação do segundo grau, seja ela completa ou incompleta. Já a fatoração e a soma e produto são mais eficientes para equações incompletas ou completas com raízes facilmente identificáveis.
A fatoração se baseia em encontrar dois binômios cujo produto resulta na equação original, enquanto a soma e produto utiliza as relações entre os coeficientes da equação e suas raízes. A fórmula de Bhaskara, por sua generalidade, é muitas vezes considerada o método mais robusto, embora possa ser mais trabalhosa em alguns casos.
Resolução de Equação Completa pela Fórmula de Bhaskara

Consideremos a equação do segundo grau completa: 2x² + 5x – 3 = Para resolvê-la pela fórmula de Bhaskara, identificamos os coeficientes: a = 2, b = 5 e c = –
3. Substituindo esses valores na fórmula
x = (-b ± √(b²
4ac)) / 2a
temos:
x = (-5 ± √(5²
- 4
- 2
- -3)) / (2
- 2)
x = (-5 ± √(25 + 24)) / 4
x = (-5 ± √49) / 4
x = (-5 ± 7) / 4
Portanto, as raízes são:
x₁ = (-5 + 7) / 4 = 2 / 4 = 1/2
x₂ = (-5 – 7) / 4 = -12 / 4 = -3
As soluções da equação são x = 1/2 e x = -3.
Resolução de Equação Incompleta pela Fatoração

Vamos resolver a equação incompleta x²
9 = 0 utilizando a fatoração. Observe que essa equação é uma diferença de quadrados, que pode ser fatorada como
(x + 3)(x – 3) = 0
Para que o produto seja zero, pelo menos um dos fatores deve ser zero. Assim, temos duas equações:
x + 3 = 0 => x = -3
x – 3 = 0 => x = 3
As soluções da equação são x = 3 e x = -3.
Problemas Práticos Modelados por Equações do 2º Grau
Equações do segundo grau são amplamente utilizadas para modelar situações reais. Um exemplo clássico é o cálculo da trajetória de um projétil. Suponha que um objeto é lançado verticalmente para cima com velocidade inicial de 20 m/s. A altura (h) em função do tempo (t) é dada pela equação: h(t) = -5t² + 20t, onde h é a altura em metros e t é o tempo em segundos.
Para determinar o tempo que o objeto leva para atingir o solo (h = 0), resolvemos a equação:
-5t² + 20t = 0
Fatorando, temos:
-5t(t – 4) = 0
As soluções são t = 0 (momento do lançamento) e t = 4 (tempo para atingir o solo). Outro exemplo seria o cálculo das dimensões de um terreno retangular, dadas sua área e o comprimento em função da largura, resultando em uma equação do segundo grau para a resolução.
Análise do Discriminante e Natureza das Raízes
A compreensão da natureza das raízes de uma equação do segundo grau é fundamental para a sua resolução e interpretação. Essa análise se baseia no cálculo do discriminante, também conhecido como delta (Δ), que nos fornece informações cruciais sobre a quantidade e o tipo de soluções da equação.O discriminante (Δ) é uma parte essencial da fórmula resolvente da equação do segundo grau, definida como Δ = b²4ac, onde a, b e c são os coeficientes da equação ax² + bx + c = 0.
O valor de Δ determina a natureza das raízes, indicando se são reais e distintas, reais e iguais, ou complexas.
O Discriminante e a Natureza das Raízes

O valor do discriminante classifica as raízes da equação em três categorias:
- Δ > 0 (Delta maior que zero): Neste caso, a equação possui duas raízes reais e distintas. Isso significa que existem dois valores diferentes de x que satisfazem a equação. Exemplo: x²
-5x + 6 = 0. Aqui, a = 1, b = -5, c = 6. Calculando Δ = (-5)²
-4(1)(6) = 25 – 24 = 1.Como Δ > 0, a equação possui duas raízes reais e distintas (x = 2 e x = 3).
- Δ = 0 (Delta igual a zero): Quando o discriminante é igual a zero, a equação possui duas raízes reais e iguais (uma raiz dupla). Geometricamente, isso significa que a parábola da função quadrática correspondente tangencia o eixo x em apenas um ponto. Exemplo: x²
-4x + 4 = 0. Aqui, a = 1, b = -4, c = 4. Calculando Δ = (-4)²
-4(1)(4) = 16 – 16 = 0.A equação possui duas raízes reais e iguais (x = 2).
- Δ < 0 (Delta menor que zero): Se o discriminante for negativo, a equação não possui raízes reais. As raízes são números complexos conjugados. Isso significa que não há pontos de interseção entre a parábola da função quadrática e o eixo x. Exemplo: x² + 2x + 5 = 0. Aqui, a = 1, b = 2, c = 5.
Calculando Δ = (2)²
-4(1)(5) = 4 – 20 = -16. Como Δ < 0, a equação possui duas raízes complexas.
Raízes Iguais e Significado Geométrico, Equação Do 2º Grau: O Que São, Tipos, Como Resolver
Quando as raízes são iguais (Δ = 0), a parábola da função quadrática y = ax² + bx + c é tangente ao eixo x. Isso significa que a parábola toca o eixo x em apenas um ponto, que é o vértice da parábola. Este ponto representa a raiz dupla da equação. A equação do eixo de simetria da parábola é dada por x = -b/2a, que coincide com a abscissa do vértice e com o valor da raiz dupla quando Δ = 0.
Gráfico da Função Quadrática e Natureza das Raízes
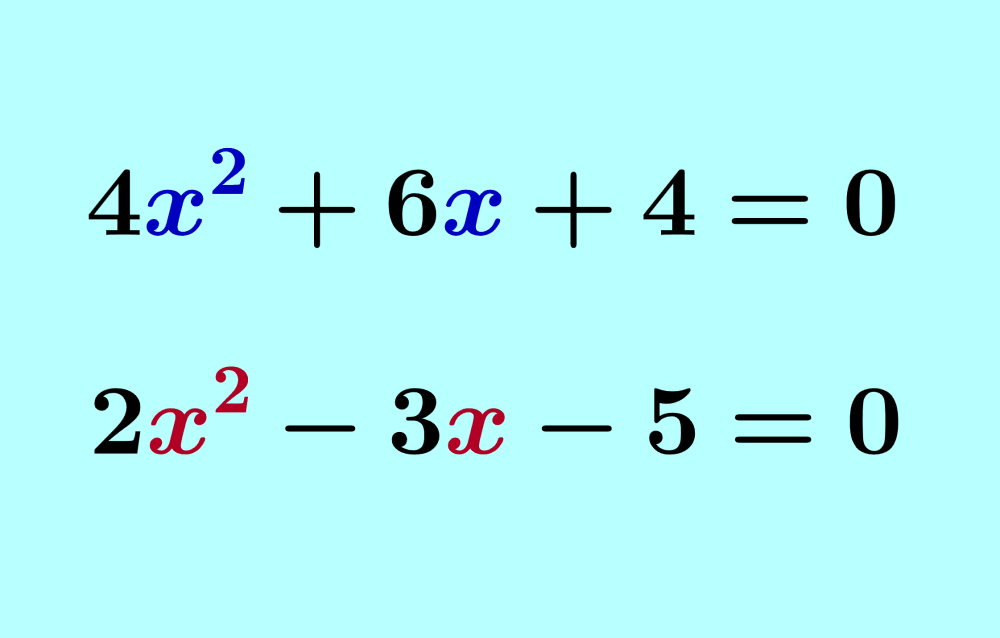
O gráfico da função quadrática y = ax² + bx + c é uma parábola. A relação entre o gráfico e a natureza das raízes da equação ax² + bx + c = 0 é direta:
- Duas raízes reais e distintas (Δ > 0): A parábola intercepta o eixo x em dois pontos distintos. As abscissas desses pontos representam as raízes da equação.
- Duas raízes reais e iguais (Δ = 0): A parábola tangencia o eixo x em um único ponto, que corresponde à raiz dupla.
- Raízes complexas (Δ < 0): A parábola não intercepta o eixo x. A parábola está totalmente acima ou totalmente abaixo do eixo x, dependendo do sinal de ‘a’.
Dominar a equação do segundo grau é abrir portas para a compreensão de conceitos matemáticos mais avançados e para a resolução de problemas do mundo real. De problemas de física envolvendo trajetórias de projéteis a questões econômicas que modelam crescimento populacional, a capacidade de resolver equações do segundo grau é essencial. Esperamos que este texto tenha fornecido uma base sólida para você se aprofundar nesse tema tão importante e aplicá-lo em diversas situações.

