Grandezas Vetoriais: Uma Introdução: Entre As Grandezas Discritar Abaixo É Exemplo De Grandeza Vetorial
Entre As Grandezas Discritar Abaixo É Exemplo De Grandeza Vetorial – Grandezas vetoriais são elementos fundamentais na física e em diversas áreas da engenharia, representando magnitudes que possuem não apenas valor numérico (módulo), mas também direção e sentido. Compreender suas propriedades e operações é crucial para modelar e resolver uma ampla gama de problemas, desde o movimento de projéteis até o comportamento de campos eletromagnéticos.
Definição e Características de Grandezas Vetoriais
Uma grandeza vetorial é definida como uma grandeza física que necessita de módulo, direção e sentido para ser completamente descrita. O módulo representa o tamanho da grandeza, a direção indica a linha de ação, e o sentido especifica o avanço ao longo dessa linha. Em contraste com as grandezas escalares, que são completamente definidas por um único valor numérico (como massa, temperatura, ou tempo), as grandezas vetoriais requerem uma descrição mais completa para sua representação.
Comparação entre Grandezas Vetoriais e Escalares
A principal diferença entre grandezas vetoriais e escalares reside na sua representação. Grandezas escalares são completamente definidas por um número e uma unidade, enquanto grandezas vetoriais requerem módulo, direção e sentido. Por exemplo, a massa de um objeto (5 kg) é uma grandeza escalar, enquanto a força aplicada sobre ele (10 N, para cima) é uma grandeza vetorial.
Tabela Comparativa de Grandezas Vetoriais
| Grandeza Vetorial | Unidade SI | Exemplo | Descrição |
|---|---|---|---|
| Deslocamento | metro (m) | Um carro se move 10m para leste. | Mudança de posição. |
| Velocidade | metro por segundo (m/s) | Um avião voa a 800 m/s para noroeste. | Taxa de variação do deslocamento. |
| Aceleração | metro por segundo ao quadrado (m/s²) | Um objeto cai com aceleração de 9.8 m/s² para baixo. | Taxa de variação da velocidade. |
| Força | newton (N) | Uma força de 50 N é aplicada para a direita em um bloco. | Interação que causa aceleração. |
| Momento Angular | quilograma metro quadrado por segundo (kg·m²/s) | Uma roda girando em torno de seu eixo. | Medida da rotação de um corpo. |
Representação Gráfica de Grandezas Vetoriais
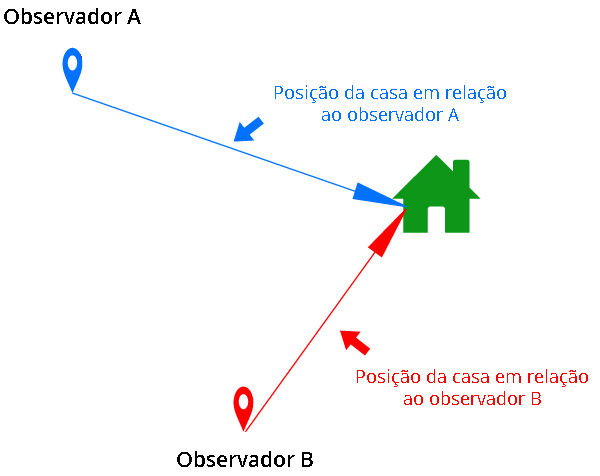
Uma grandeza vetorial é graficamente representada por uma seta. O comprimento da seta é proporcional ao módulo do vetor, a direção da seta indica a direção do vetor, e a ponta da seta indica o sentido do vetor. Um vetor nulo é representado por uma seta de comprimento zero, indicando ausência de magnitude. Um vetor unitário possui módulo igual a 1, servindo como base para a definição de outras grandezas vetoriais.
Soma Vetorial: Métodos Gráficos
A soma vetorial pode ser realizada graficamente através do método do paralelogramo ou do método ponta-a-cauda. No método do paralelogramo, os vetores são posicionados com a origem comum, e a resultante é a diagonal do paralelogramo formado. No método ponta-a-cauda, a origem de um vetor é posicionada na ponta do outro, e a resultante é o vetor que liga a origem do primeiro vetor à ponta do segundo.
Operações com Vetores
Além da adição, a subtração de vetores pode ser entendida como a adição do vetor oposto. A multiplicação de um vetor por um escalar altera apenas o módulo do vetor, mantendo a direção. O produto escalar resulta em um escalar, representando a projeção de um vetor sobre outro. O produto vetorial resulta em um novo vetor perpendicular aos vetores originais, com módulo relacionado ao seno do ângulo entre eles.
Adição e Subtração Vetorial, Entre As Grandezas Discritar Abaixo É Exemplo De Grandeza Vetorial
A adição vetorial é realizada somando-se as componentes correspondentes dos vetores. A subtração é similar, subtraindo-se as componentes correspondentes. Diagramas vetoriais ilustram esses processos, mostrando a resultante como a diagonal do paralelogramo na adição e a diferença como o vetor que fecha o triângulo na subtração.
Produto Escalar e Vetorial
O produto escalar de dois vetores A e B é calculado como A.B = |A||B|cosθ, onde θ é o ângulo entre os vetores. O produto vetorial A x B resulta em um vetor C com módulo |A||B|senθ, direção perpendicular ao plano formado por A e B, e sentido dado pela regra da mão direita.
Aplicações de Grandezas Vetoriais na Física
Grandezas vetoriais são essenciais para descrever fenômenos físicos. Na cinemática, elas descrevem o movimento de corpos; na dinâmica, elas descrevem as forças e suas interações; e no eletromagnetismo, elas descrevem campos elétricos e magnéticos.
Exemplos de Problemas Físicos
Um exemplo clássico é o lançamento de projéteis, onde a velocidade inicial, a aceleração da gravidade e a força de resistência do ar são grandezas vetoriais que determinam a trajetória do projétil. Outro exemplo é a análise de circuitos elétricos, onde correntes e campos elétricos são representados por vetores.
Aplicações na Engenharia
- Engenharia Civil: Cálculo de esforços em estruturas, análise de tensões e deformações.
- Engenharia Mecânica: Análise de forças em mecanismos, projeto de sistemas de transmissão de potência.
- Engenharia Elétrica: Análise de circuitos elétricos, projeto de sistemas de potência.
Componentes de um Vetor
Um vetor pode ser decomposto em suas componentes cartesianas (x, y, z), representando suas projeções nos eixos coordenados. O módulo do vetor é calculado pela raiz quadrada da soma dos quadrados de suas componentes. A direção é determinada pelos ângulos que o vetor forma com os eixos coordenados.
Tabela de Vetores e Componentes Cartesianas
| Vetor | Componentes Cartesianas |
|---|---|
| A = (3, 4, 0) | Ax = 3, Ay = 4, Az = 0 |
| B = (-2, 1, 5) | Bx = -2, By = 1, Bz = 5 |
Exemplos de Grandezas Vetoriais no Cotidiano
A compreensão de grandezas vetoriais facilita a análise de diversas situações do dia a dia. Por exemplo, ao jogar uma bola, o arremesso envolve a velocidade e a força, ambos vetores que influenciam na trajetória e no alcance da bola.
Exemplos Cotidianos

- Deslocamento de um carro: Módulo: distância percorrida, Direção: rota, Sentido: direção do movimento.
- Velocidade do vento: Módulo: intensidade do vento, Direção: direção do vento, Sentido: sentido do vento.
- Força aplicada ao empurrar uma porta: Módulo: intensidade da força, Direção: perpendicular à porta, Sentido: para dentro ou para fora.
- Força de atrito: Módulo: força resistiva, Direção: oposta ao movimento, Sentido: contrário ao movimento.
- Velocidade de um rio: Módulo: velocidade da água, Direção: direção do fluxo, Sentido: sentido do fluxo.
Concluímos nossa exploração do universo das grandezas vetoriais com uma compreensão mais profunda de sua importância e aplicabilidade. De situações cotidianas, como o lançamento de uma bola, até complexos cálculos em engenharia e física, as grandezas vetoriais são ferramentas essenciais para descrever e analisar fenômenos físicos com precisão. Dominar seus conceitos, desde a representação gráfica até as operações vetoriais, é fundamental para qualquer pessoa que busca uma compreensão mais abrangente do mundo ao seu redor.
Esperamos que esta jornada tenha sido esclarecedora e estimulante, impulsionando sua curiosidade e seu desejo de aprofundar seus conhecimentos nessa área tão rica e relevante.

