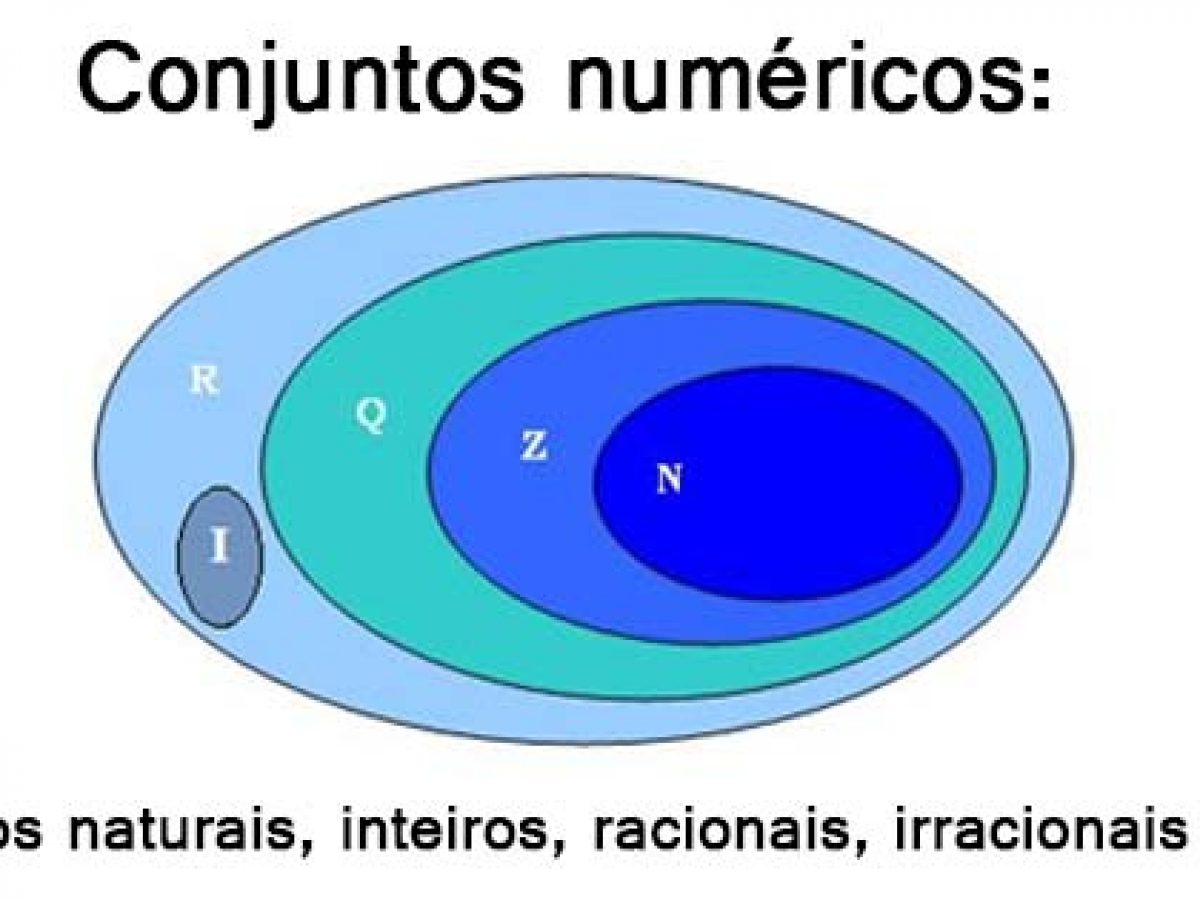
É Um Exemplo De Número Irracional: Escolha Uma: traz um mergulho fascinante no mundo dos números irracionais, aqueles que não podem ser expressos como uma fração de dois números inteiros. Prepare-se para descobrir a natureza elusiva desses números e sua presença intrigante em nosso universo.
A jornada começa com uma definição clara de números irracionais, seguida de exemplos concretos que ilustram sua singularidade. Em seguida, o texto explora a prova de que a raiz quadrada de 2 é um número irracional, demonstrando o método da prova por contradição.
Número Irracional
Um número irracional é um número real que não pode ser expresso como uma fração de dois números inteiros. Em outras palavras, é um número decimal que não termina nem se repete.
Alguns exemplos de números irracionais:
- Pi (π): O número pi é a razão entre o perímetro de um círculo e seu diâmetro. É um número irracional que foi calculado com precisão para bilhões de casas decimais.
- A raiz quadrada de 2: A raiz quadrada de 2 é o comprimento da diagonal de um quadrado com lados de comprimento 1. É um número irracional que foi provado por Pitágoras no século VI a.C.
- O número áureo: O número áureo é um número irracional que é aproximadamente igual a 1,618. É encontrado em muitas formas naturais e tem sido usado em arte e arquitetura por séculos.
Raiz Quadrada de 2: É Um Exemplo De Número Irracional: Escolha Uma:

A raiz quadrada de 2 é um número irracional, o que significa que não pode ser expresso como uma fração de dois números inteiros. Em outras palavras, é um número decimal não periódico e não terminante.
Prova por Contradição
Para provar que a raiz quadrada de 2 é irracional, podemos usar o método da prova por contradição. Suponhamos, por absurdo, que a raiz quadrada de 2 seja racional. Isso significa que ela pode ser escrita como uma fração de dois números inteiros, ou seja, √2 = a/b, onde a e b são inteiros e b ≠ 0.Elevando
ambos os lados da equação ao quadrado, obtemos:
= a²/b²
a² = 2b²Isso implica que a² é par, pois é igual a 2b². Mas como a² é o quadrado de um número inteiro, ele também deve ser par. Portanto, a deve ser par.Como a é par, podemos escrever a = 2k, onde k é um número inteiro.
Substituindo em a² = 2b², obtemos:(2k)² = 2b²
- k² = 2b²
- k² = b²
Isso implica que b² é par, pois é igual a 2k². Mas como b² é o quadrado de um número inteiro, ele também deve ser par. Portanto, b deve ser par.O fato de a e b serem ambos pares contradiz a suposição inicial de que a fração a/b é irredutível (ou seja, não pode ser simplificada).
Portanto, nossa suposição original de que √2 é racional deve ser falsa.Concluímos, então, que a raiz quadrada de 2 é um número irracional.
Propriedades dos Números Irracionais
Os números irracionais possuem propriedades únicas que os distinguem dos números racionais. Vamos explorá-las e compará-las com os números racionais.
Não São Racionais
A propriedade fundamental dos números irracionais é que eles não podem ser expressos como uma fração de dois números inteiros. Isso significa que eles não podem ser escritos na forma a/b, onde ae bsão números inteiros e bnão é zero.
Decimais Não Periódicos
Outra propriedade dos números irracionais é que suas representações decimais são não periódicas. Isso significa que seus dígitos decimais não se repetem em um padrão regular. Por exemplo, a representação decimal de π (3,14159…) nunca se repete.
Comparação com Números Racionais, É Um Exemplo De Número Irracional: Escolha Uma:
Em contraste com os números irracionais, os números racionais são aqueles que podem ser expressos como uma fração de dois números inteiros. Eles têm representações decimais periódicas, onde os dígitos decimais se repetem em um padrão regular. Além disso, os números racionais podem ser representados como números decimais finitos ou não finitos.
Aplicações dos Números Irracionais

Os números irracionais encontram aplicações em diversos campos, incluindo:
Ciências Naturais
- Física:O número pi (π) é usado para calcular o perímetro e a área de círculos, enquanto a raiz quadrada de 2 (√2) é usada para calcular as diagonais de quadrados.
- Biologia:A sequência de Fibonacci, que é uma sequência de números irracionais, é encontrada em padrões de crescimento em plantas e animais.
Engenharia
- Arquitetura:O número áureo (φ) é usado para criar proporções harmoniosas em edifícios e outras estruturas.
- Engenharia Elétrica:A impedância de um circuito é um número irracional que afeta o fluxo de corrente.
Matemática
- Geometria:Os números irracionais são usados para calcular as áreas e volumes de figuras geométricas, como esferas e cones.
- Trigonometria:As funções seno, cosseno e tangente usam números irracionais para representar ângulos.
Concluindo, É Um Exemplo De Número Irracional: Escolha Uma: oferece uma compreensão abrangente das propriedades e aplicações dos números irracionais. Eles são uma parte essencial da matemática, encontrados em campos tão diversos quanto geometria, física e engenharia. Sua natureza elusiva os torna objetos de fascínio contínuo, inspirando novas descobertas e avanços no reino dos números.