Prismas de Base Poligonal: Uma Exploração Geométrica: 1 Exemplo Prisma De Base Poligonal Atura Perimetro Area Total
Exemplo Prisma De Base Poligonal Atura Perimetro Area Total – Prismas, sólidos geométricos fascinantes, são objetos tridimensionais com bases poligonais paralelas e congruentes, conectadas por faces laterais que são paralelogramos. Compreender suas propriedades, como perímetro, área da base e área total, é fundamental em diversas áreas, desde a arquitetura à engenharia.
Introdução ao Prisma de Base Poligonal
Um prisma de base poligonal é caracterizado por duas bases poligonais idênticas e paralelas, conectadas por faces laterais que são paralelogramos. A forma da base determina o nome do prisma (triangular, quadrangular, pentagonal, etc.). A distância entre as bases é a altura do prisma. Prismas retos possuem faces laterais perpendiculares às bases, enquanto prismas oblíquos apresentam faces laterais inclinadas.
Um exemplo de prisma reto é uma caixa de sapatos, enquanto um prisma oblíquo poderia ser representado por uma pilha de livros ligeiramente empilhados de forma inclinada.
A relação entre a base, a altura e as faces laterais é direta: a área da base multiplicada pela altura determina o volume do prisma, enquanto o perímetro da base multiplicado pela altura determina a área lateral.
Cálculo do Perímetro da Base
O perímetro de uma base poligonal é a soma dos comprimentos de todos os seus lados. Para polígonos regulares, onde todos os lados têm o mesmo comprimento, o cálculo é simplificado: perímetro = número de lados × comprimento do lado. Polígonos irregulares exigem a soma individual de cada lado.
Por exemplo, um quadrado com lados de 5 cm tem um perímetro de 20 cm (4 lados × 5 cm/lado). Um triângulo com lados de 3 cm, 4 cm e 5 cm tem um perímetro de 12 cm.
| Polígono | Comprimento dos Lados | Cálculo do Perímetro | Perímetro |
|---|---|---|---|
| Triângulo Equilátero | 3 cm, 3 cm, 3 cm | 3 + 3 + 3 | 9 cm |
| Quadrado | 4 cm, 4 cm, 4 cm, 4 cm | 4 + 4 + 4 + 4 | 16 cm |
| Pentágono Regular | 2 cm, 2 cm, 2 cm, 2 cm, 2 cm | 2 + 2 + 2 + 2 + 2 | 10 cm |
Cálculo da Área da Base, 1 Exemplo Prisma De Base Poligonal Atura Perimetro Area Total

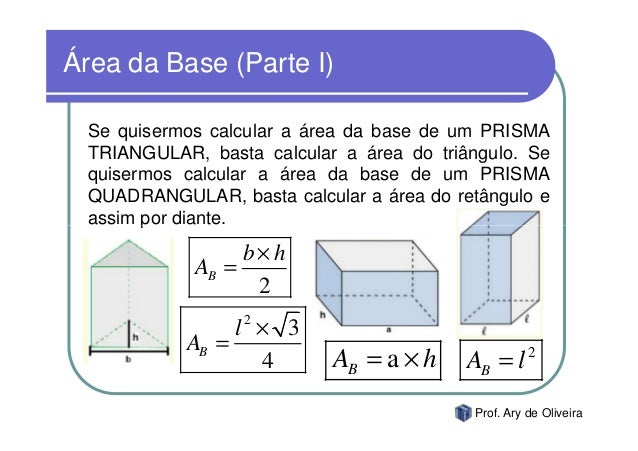
O cálculo da área da base varia de acordo com o tipo de polígono. Para um quadrado, a área é lado². Para um triângulo, é (base × altura)/2. Polígonos regulares mais complexos podem exigir fórmulas mais elaboradas ou a decomposição em triângulos. Polígonos irregulares frequentemente necessitam de métodos mais complexos, como a decomposição em figuras geométricas mais simples cujas áreas são conhecidas.
Comparando o cálculo da área de um quadrado e de um triângulo, observamos que o quadrado, com sua fórmula simples, é mais fácil de calcular. Já o triângulo exige a identificação da altura, o que pode ser mais complexo em triângulos irregulares.
Cálculo da Área Lateral e Área Total

A área lateral de um prisma é calculada multiplicando o perímetro da base pela altura do prisma. A área total é a soma da área lateral e o dobro da área da base (já que existem duas bases).
- Calcule o perímetro da base.
- Calcule a área da base.
- Multiplique o perímetro da base pela altura do prisma para obter a área lateral.
- Multiplique a área da base por 2.
- Some a área lateral e o dobro da área da base para obter a área total.
Exemplo Prático: Prisma de Base Triangular
Considere um prisma reto com base triangular equilátera de lado 6 cm e altura do prisma de 10 cm. A base triangular é um triângulo equilátero, formando um prisma triangular reto. Visualmente, imagine uma pirâmide triangular com a ponta “cortada” paralelamente à base, resultando em duas bases triangulares congruentes e três faces laterais retangulares.
| Parâmetro | Cálculo | Resultado | Unidade |
|---|---|---|---|
| Perímetro da base | 6 cm + 6 cm + 6 cm | 18 cm | cm |
| Área da base | (6 cm × (6√3)/2 cm) | 15,59 cm² | cm² |
| Área lateral | 18 cm × 10 cm | 180 cm² | cm² |
| Área total | 180 cm² + 2 × 15,59 cm² | 211,18 cm² | cm² |
Exemplo Prático: Prisma de Base Quadrada
Consideremos um prisma reto com base quadrada de lado 5 cm e altura de 8 cm. Imagine um cubo cortado ao meio paralelamente a duas faces opostas. As duas metades resultantes são prismas de base quadrada.
Comparando com o prisma triangular, o cálculo do prisma quadrado é mais direto devido à simplicidade da geometria da base quadrada. Ambos os cálculos, no entanto, seguem os mesmos princípios gerais de cálculo de perímetro, área da base, área lateral e área total.
Ilustração de um Prisma de Base Pentagonal
Um prisma de base pentagonal regular possui duas bases pentagonais idênticas e paralelas, conectadas por cinco faces laterais retangulares em um prisma reto. Cada ângulo interno do pentágono regular mede 108 graus, e todos os lados possuem o mesmo comprimento. Em um prisma reto, as faces laterais são perpendiculares às bases. Imagine um sólido com duas bases pentagonais congruentes, com cinco retângulos conectando-as lateralmente, formando um prisma com 7 faces, 10 vértices e 15 arestas.
A área de uma face pentagonal regular pode ser calculada dividindo-a em cinco triângulos isósceles congruentes, calculando a área de um triângulo e multiplicando por cinco.
Em resumo, calcular a área e o perímetro de um prisma de base poligonal, embora pareça complexo à primeira vista, torna-se um processo simples e lógico ao se entender os princípios básicos e aplicar as fórmulas adequadas. De prismas com bases triangulares a pentagonais, a metodologia apresentada neste guia demonstra a versatilidade e a aplicabilidade dos conceitos geométricos em situações reais.
Esperamos que esta exploração tenha sido esclarecedora e que você agora se sinta confiante para enfrentar qualquer desafio envolvendo o cálculo de áreas e perímetros de prismas. A prática é fundamental, então, não hesite em aplicar o que aprendeu a diferentes exemplos e aprofundar seus conhecimentos neste fascinante campo da matemática.

